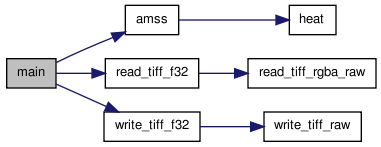
amss/FDS_AMSS.c File Reference

Finite Difference Scheme for the Affine Morphological Scale Space. More...

#include <stdlib.h>
#include <tiffio.h>
#include <time.h>
#include <math.h>
#include "io_tiff_routine.h"

Include dependency graph for FDS_AMSS.c:

This graph shows which files directly or indirectly include this file:

Defines
#define	FATAL(MSG)
#define	INFO(MSG)
#define	DEBUG(MSG)
Functions
static void	heat (float ptr_out, float ptr_in, size_t n_col, int i, int i_prev, int i_next, int j, int j_prev, int j_next, float dt)
	Computes one iteration of Heat Equation.
static void	amss (float ptr_out, float ptr_in, size_t n_row, size_t n_col, float dt, float t_g)
	Computes one iteration of the Affine Morphological Scale Space.
int	main (int argc, char *argv[])
	main function call

Detailed Description

Finite Difference Scheme for the Affine Morphological Scale Space.

Version:: 1.3

Author:: Adina Ciomaga; <adina.ciomaga@cmla.ens-cachan.fr>; Marco Mondelli; <m.mondelli@sssup.it>

requirements:

ANSI C compiler
libtiff

compilation:

type "gcc FDS_AMSS.c io_tiff_all.c -ltiff -o amss.out" to obtain the executable file
type "amss.out" followed by the required arguments to run the executable file

usage: this programs requires 3 arguments written in the following order,

argv[1] contains the normalized scale you want to reach
argv[2] contains the name of the input file
argv[3] contains the name of the output file

The normalized scale represents the scale 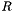$ R $ at which a circle with radius 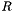$ R $ disappears. The number of iterations needed is linked to normalized scale and time step by the following formula:

$n_{iter}= \frac {3}{4 \cdot dt} R^{\frac{4}{3}}$

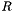where $ R $ is the normalized scale, 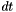$ dt $ the time step and 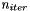$n_{iter}$ the number of iterations.

Definition in file FDS_AMSS.c.

Define Documentation

#define DEBUG ( MSG )

Value:

do {\
        if (debug_flag)\
            fprintf(stderr, __FILE__ ":%03i " MSG "\n", __LINE__);\
    } while (0);

print a debug message, with detailed information

Definition at line 95 of file FDS_AMSS.c.

#define FATAL ( MSG )

Value:

do {\
          fprintf(stderr, MSG "\n");\
        abort();\
        } while (0);

print a message and abort the execution

Definition at line 82 of file FDS_AMSS.c.

#define INFO ( MSG )

Value:

do {\
        fprintf(stderr, MSG "\n");\
    } while (0);

print an info message

Definition at line 89 of file FDS_AMSS.c.

Function Documentation

static void amss	(	float *	ptr_out,
		float *	ptr_in,
		size_t	n_row,
		size_t	n_col,
		float	dt,
		float	t_g
	)			`[static]`

Computes one iteration of the Affine Morphological Scale Space.

This function applies a Finite Difference Scheme for Affine Curvature Motion

$u_t=|Du|(curv(u))^{\frac{1}{3}}= (|Du|^3 curv(u))^{\frac{1}{3}}$

Similarly to MCM, when 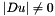$|Du| \neq 0$ , we denote by 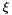$\xi$ the direction orthogonal to 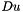$ Du $ and by 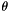$\theta$ the angle between the 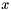$ x $ positive semiaxis and the gradient. Hence

$u_{\xi\xi}=D^2u(\xi,\xi)=D^2u\Bigl(\frac{Du^{\perp}}{|Du|},\frac{Du^{\perp}} {|Du|}\Bigr)= \frac{1}{|Du|^2}D^2u(Du^{\perp},Du^{\perp})= |Du|curv(u)$

and the continuous equation can be translated in this discrete version:

$u_{n+1}(i,j)= u_n(i,j) + + \Delta t \cdot (|Du_n|^2 (u_{\xi\xi})_n)^{\frac{1}{3}}(i,j)$

As regards the numerical evaluation of 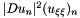$|Du_n|^2 (u_{\xi\xi})_n$ , we adopt a linear finite difference scheme based on a 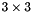$3 \times 3$ stencil.

$|Du_n|^2 (u_{\xi\xi})_n (i,j)=\frac{1}{\Delta x^2}( \hspace{0.3em} -4\eta_0 \cdot u_n(i,j)\hspace{0.3em} + \hspace{0.3em} \eta_1 \cdot (u_n(i,j+1) + u_n(i,j-1)) \hspace{0.3em} + \hspace{0.3em} \eta_2 \cdot (u_n(i+1,j) + u_n(i-1,j)) \hspace{0.3em} + \hspace{0.3em} \eta_3 \cdot (u_n(i-1,j-1) + u_n(i+1,j+1)) \hspace{0.3em} + \hspace{0.3em} \eta_4 \cdot (u_n(i-1,j+1) + u_n(i+1,j-1)) \hspace{0.3em})$

which can be rewritten in a more synthetic form, using a discrete convolution with a variable kernel $ B $

$|Du_n|^2 (u_{\xi\xi})_n=\frac{1}{\Delta x^2}\cdot (B \star u_n) \quad \mbox{where} \quad B=\Biggl( \begin{array}{ccc} \eta_3(\theta) & \eta_2(\theta) & \eta_4(\theta) \\ \eta_1(\theta) & -4\eta_0(\theta) & \eta_1(\theta) \\ \eta_4(\theta) & \eta_2(\theta) & \eta_3(\theta) \end{array} \Biggr)$

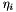We talk about $\emph{variable kernel}$ since the $\eta_i$ depend on the direction of 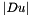$ |Du| $ and can be calculated directly from the FDS of the partial derivatives 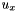$ u_x $ and $ u_y $ .

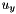$\begin{array}{l} u_x= \displaystyle \frac{2\cdot (u(i,j+1) - u(i,j-1)) + u(i-1,j+1) - u(i-1,j-1) + u(i+1,j+1) - u(i+1,j-1)} {8\Delta x}= \displaystyle \frac{s_x}{8\Delta x} \\ \\ u_y= \displaystyle \frac{2\cdot (u(i+1,j) - u(i-1,j)) + u(i+1,j+1) - u(i-1,j+1) + u(i+1,j-1) - u(i-1,j-1)} {8\Delta x}= \displaystyle \frac{s_y}{8\Delta x} \\ \end{array}$

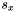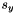where we have denoted respectively by $ s_x $ and $ s_y $ the algebric sums at the numerator of 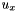$ u_x $ and $ u_y $ .

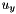A very similar procedure is followed if we want to obtain an algorithm for MCM. The only difference is that for the Mean Curvature Motion we must discretize only 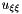$u_{\xi \xi}$ , which can be seen again as the result of a convolution with a discrete kernel $ A $ :

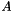$u_{\xi\xi_n}=\frac{1}{\Delta x^2}\cdot (A \star u_n) \quad \mbox{where} \quad A=\Biggl(\begin{array}{ccc} \lambda_3(\theta) & \lambda_2(\theta) & \lambda_4(\theta) \\ \lambda_1(\theta) & -4\lambda_0(\theta) & \lambda_1(\theta) \\ \lambda_4(\theta) & \lambda_2(\theta) & \lambda_3(\theta) \end{array} \Biggr)$

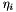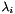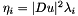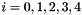Thus the choice of the $\eta_i$ can be reduced to that of the $\lambda_i$ , since $\eta_i= |Du|^2 \lambda_i$ for $ i=0,1,2,3,4 $ . Experiments have shown that if we take 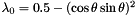$\lambda_0= 0.5- (\cos\theta \sin\theta)^2$ , i.e. the same value used in MCM, the best results as regards stability are achieved. Therefore the following formulas are actually adopted in the algorithm:

$\begin{array}{l} \eta_0=\displaystyle\frac{1}{2} \cdot (u_x^2+u_y^2)-\frac{u_x^2 \cdot u_y^2} {u_x^2+u_y^2} \\ \\ \eta_1= 2\eta_0 - u_x^2 \\ \\ \eta_2= 2\eta_0 - u_y^2 \\ \\ \eta_3= -\eta_0 + \displaystyle \frac{1}{2} \cdot (u_x^2 + u_y^2 - u_x \cdot u_y) \\ \\ \eta_4= -\eta_0 + \displaystyle \frac{1}{2} \cdot (u_x^2 + u_y^2 + u_x \cdot u_y) \end{array}$

Remember that the array representing the image is examinated as a matrix, i.e. 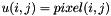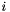$ u(i,j)=pixel(i,j) $ : $ i $ is the current row number and 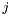$ j $ is the current column number. The infinitezimal 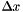$\Delta x$ is the pixel width and is set to $ 1 $ .

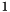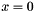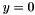On the border, we symmetrize the image with respect to the axes $ x=0 $ and $ y=0 $ , i.e.

$\begin{array}{l} u(-1,j) = u(0,j) \\ \\ u(n_{row},j) = u(n_{row}-1,j) \\ \\ u(i,-1) = u(i,0) \\ \\ u(i,n_{col}) = u(i,n_{col}-1) \end{array}$

From a theorical point of view, even if we divide by the gradient, there is no need to apply Heat Equation when 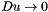$Du \rightarrow 0$ .

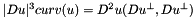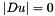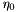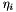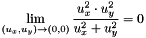In fact $|Du|^3 curv(u)= D^2u(Du^{\perp},Du^{\perp})$ and, if $ |Du|=0 $ the Affine Morphological Scale Space is well defined. In addition even $\eta_0$ and consequently all the $\eta_i$ are well defined in the limit, since $\displaystyle \lim_{(u_x,u_y) \to (0,0)} \frac{u_x^2 \cdot u_y^2}{u_x^2+u_y^2}=0$ .

However rounding and approximation errors lead us to replace AMSS with Heat Equation when the gradient is below a threshold (experimentally set to 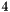$ 4 $ for the first iteration and then reduced to 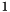$ 1 $ for the next ones).

Parameters:

`[out]`	ptr_out	pointer to the output array
`[in]`	ptr_in	pointer to the input array
`[in]`	n_row	number of rows
`[in]`	n_col	number of columns
`[in]`	dt	time step
`[in]`	t_g	threshold for the gradient

Definition at line 301 of file FDS_AMSS.c.

Here is the call graph for this function:

Here is the caller graph for this function:

static void heat	(	float *	ptr_out,
		float *	ptr_in,
		size_t	n_col,
		int	i,
		int	i_prev,
		int	i_next,
		int	j,
		int	j_prev,
		int	j_next,
		float	dt
	)			`[static]`

Computes one iteration of Heat Equation.

This function applies the following Finite Difference Scheme for Heat Equation

$u_{n+1} = u_n + dt \cdot \Delta u_n$

where the discrete laplacian 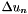$\Delta u_n$ is given by

$\Delta u_n = u_n(i+1,j) + u_n(i-1,j) + u_n(i,j+1) + u_n(i,j-1) - 4u_n(i,j)$

Parameters:

`[out]`	ptr_out	pointer to the output array
`[in]`	ptr_in	pointer to the input array
`[in]`	n_col	number of columns
	i	current row
	i_prev	previous row
	i_next	next row
	j	current column
	j_prev	previous column
	j_next	next column
`[in]`	dt	time step

Definition at line 135 of file FDS_AMSS.c.

Here is the caller graph for this function:

int main	(	int	argc,
		char *	argv[]
	)

main function call

The program reads an image.tiff given as input, applies a Finite Difference Scheme for the Affine Morphological Scale Space at renormalized scale 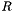$ R $ , writes the result as a new image.tiff and returns it as output.

Definition at line 380 of file FDS_AMSS.c.

Here is the call graph for this function:

amss/FDS_AMSS.c File Reference

Defines

Functions

Detailed Description

Define Documentation

Function Documentation