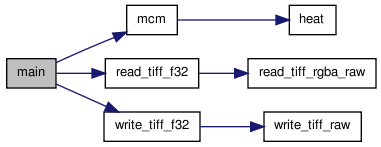
mcm/FDS_MCM.c File Reference

Finite Difference Scheme for the Mean Curvature Motion. More...

#include <stdlib.h>
#include <tiffio.h>
#include "io_tiff_routine.h"
#include <time.h>
#include <math.h>
Include dependency graph for FDS_MCM.c:
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Defines

#define FATAL(MSG)
#define INFO(MSG)
#define DEBUG(MSG)

Functions

static void heat (float *ptr_out, float *ptr_in, size_t n_col, int i, int i_prev, int i_next, int j, int j_prev, int j_next, float dt)
 Computes one iteration of Heat Equation.
static void mcm (float *ptr_out, float *ptr_in, size_t n_row, size_t n_col, float dt, float t_g)
 Computes one iteration of the Mean Curvature Motion.
int main (int argc, char *argv[])
 Main function call.

Detailed Description

Finite Difference Scheme for the Mean Curvature Motion.

Version:
1.3
Author:
Adina Ciomaga; <adina.ciomaga@cmla.ens-cachan.fr> ;
Marco Mondelli; <m.mondelli@sssup.it>

requirements:

compilation:

usage: this programs requires 3 arguments written in the following order,

The normalized scale represents the scale 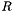$ R $ at which a circle with radius 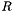$ R $ disappears. The number of iterations needed is linked to normalized scale and time step by the following formula:

\[ n_{iter}= \frac{R^2}{2 \cdot dt} \]

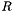where $ R $ is the normalized scale, 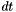$ dt $ the time step and 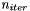$ n_{iter} $ the number of iterations.

Definition in file FDS_MCM.c.

Define Documentation

#define DEBUG ( MSG   ) 
Value:
do {\
        if (debug_flag)\
            fprintf(stderr, __FILE__ ":%03i " MSG "\n", __LINE__);\
    } while (0);

print a debug message with detailed information

Definition at line 97 of file FDS_MCM.c.

#define FATAL ( MSG   ) 
Value:
do {\
          fprintf(stderr, MSG "\n");\
        abort();\
        } while (0);

print a message and abort the execution

Definition at line 84 of file FDS_MCM.c.

#define INFO ( MSG   ) 
Value:
do {\
        fprintf(stderr, MSG "\n");\
    } while (0);

print an info message

Definition at line 91 of file FDS_MCM.c.

Function Documentation

static void heat ( float *  ptr_out,
float *  ptr_in,
size_t  n_col,
int  i,
int  i_prev,
int  i_next,
int  j,
int  j_prev,
int  j_next,
float  dt 
) [static]

Computes one iteration of Heat Equation.

This function applies the following Finite Difference Scheme for Heat Equation

\[ u_{n+1} = u_n + dt \cdot \Delta u_n \]

where the discrete laplacian 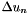$ \Delta u_n $ is given by

\[ \Delta u_n = u_n(i+1,j) + u_n(i-1,j) + u_n(i,j+1) + u_n(i,j-1) - 4u_n(i,j) \]

Parameters:
[out] ptr_out pointer to the output array
[in] ptr_in pointer to the input array
[in] n_col number of columns
i current row
i_prev previous row
i_next next row
j current column
j_prev previous column
j_next next column
[in] dt time step

Definition at line 138 of file FDS_MCM.c.

Here is the caller graph for this function:

int main ( int  argc,
char *  argv[] 
)

Main function call.

The program reads an image.tiff given as input, applies a Finite Difference Scheme for the Mean Curvature Motion at renormalized scale 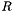$ R $, writes the result as a new image.tiff and returns it as output.

Definition at line 357 of file FDS_MCM.c.

Here is the call graph for this function:

static void mcm ( float *  ptr_out,
float *  ptr_in,
size_t  n_row,
size_t  n_col,
float  dt,
float  t_g 
) [static]

Computes one iteration of the Mean Curvature Motion.

This function applies a Finite Difference Scheme for the Mean Curvature Motion

\[ u_t=|Du|curv(u) \]

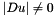When $ |Du| \neq 0 $, we denote by 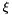$ \xi $ the direction orthogonal to 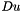$ Du $ and by 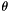$ \theta $ the angle between the 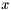$ x $ positive semiaxis and the gradient. Since

\[ u_{\xi\xi}=D^2u(\xi,\xi)=D^2u\Bigl(\frac{Du^{\perp}}{|Du|},\frac{Du^{\perp}} {|Du|}\Bigr)= \frac{1}{|Du|^2}D^2u(Du^{\perp},Du^{\perp})= |Du|curv(u) \]

the continuous equation can be translated in the followig discrete version:

\[ u_{n+1}(i,j)=u_n(i,j)+\Delta t (u_{\xi\xi})_n(i,j) \]

For the numerical evaluation of 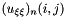$ (u_{\xi \xi})_n(i,j) $ we adopt a linear finite difference scheme based on a 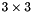$ 3 \times 3 $ stencil.

\[ (u_{\xi \xi})_n(i,j)= \frac{1}{\Delta x^2}( \hspace{0.3em} -4\lambda_0 \cdot u_n(i,j) \hspace{0.3em} + \hspace{0.3em} \lambda_1 \cdot (u_n(i,j+1) + u_n(i,j-1)) \hspace{0.3em} + \hspace{0.3em} \lambda_2 \cdot (u_n(i+1,j) + u_n(i-1,j)) \hspace{0.3em} + \hspace{0.3em} \lambda_3 \cdot (u_n(i-1,j-1) +u_n(i+1,j+1)) \hspace{0.3em} + \hspace{0.3em} \lambda_4 \cdot (u_n(i-1,j+1) +u_n(i+1,j-1)) \hspace{0.3em}) \]

The later can be rewritten in a more synthetic form, using a discrete convolution with a variable kernel 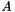$ A $

\[ u_{\xi\xi_n}=\frac{1}{\Delta x^2}\cdot (A \star u_n) \quad \mbox{where} \quad A=\Biggl(\begin{array}{ccc} \lambda_3(\theta) & \lambda_2(\theta) & \lambda_4(\theta) \\ \lambda_1(\theta) & -4\lambda_0(\theta) & \lambda_1(\theta) \\ \lambda_4(\theta) & \lambda_2(\theta) & \lambda_3(\theta) \end{array} \Biggr) \]

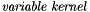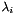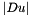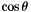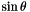We talk about $ \emph{variable kernel} $ since the $ \lambda_i $ depend on the direction of $ |Du| $ and can be calculated either from $ \cos\theta $ and $ \sin\theta\ $ or (as we do in the code to optimize the number of variables allocated) directly from the FDS of the partial derivatives 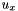$ u_x $ and $ u_y $.

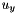\[ \begin{array}{l} u_x= \displaystyle \frac{2\cdot (u(i,j+1) - u(i,j-1)) + u(i-1,j+1) - u(i-1,j-1) + u(i+1,j+1) - u(i+1,j-1)} {8\Delta x}= \displaystyle \frac{s_x}{8\Delta x} \\ \\ u_y= \displaystyle \frac{2\cdot (u(i+1,j) - u(i-1,j)) + u(i+1,j+1) - u(i-1,j+1) + u(i+1,j-1) - u(i-1,j-1)} {8\Delta x}= \displaystyle \frac{s_y}{8\Delta x} \\ \end{array} \]

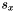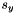where we have denoted respectively by $ s_x $ and $ s_y $ the algebric sums at the numerator of 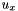$ u_x $ and $ u_y $.

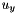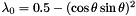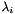With the choice $\lambda_0 = 0.5 - (\cos\theta \sin\theta)^2 $ the following formulas hold for the $ \lambda_i$:

\[ \begin{array}{l} \lambda_0= \displaystyle \frac{1}{2} - \frac{s_x^2 \cdot s_y^2} {(s_x^2+s_y^2)^2} \\ \\ \lambda_1= 2\lambda_0 - \displaystyle \frac{s_x^2}{s_x^2+s_y^2} \\ \\ \lambda_2= 2\lambda_0 - \displaystyle \frac{s_y^2}{s_x^2+s_y^2} \\ \\ \lambda_3= -\lambda_0 +\displaystyle \frac{1}{2} \cdot \Bigl(1-\frac{s_x \cdot s_y} {s_x^2+s_y^2}\Bigr) \\ \\ \lambda_4= -\lambda_0 +\displaystyle \frac{1}{2} \cdot \Bigl(1+\frac{s_x \cdot s_y} {s_x^2+s_y^2}\Bigr) \end{array} \]

Remember that the array representing the image is examinated as a matrix, i.e. 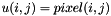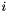$ u(i,j)=pixel(i,j) $: $ i $ is the current row number and 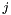$ j $ is the current column number. The infinitezimal increment 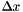$\Delta x $ is the pixel width and is set to $ 1 $.

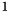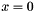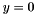At the borders, we symmetrize the image with respect to the axes $ x=0 $ and $ y=0 $, i.e.

\[ \begin{array}{l} u(-1,j) = u(0,j) \\ \\ u(n_{row},j) = u(n_{row}-1,j) \\ \\ u(i,-1) = u(i,0) \\ \\ u(i,n_{col}) = u(i,n_{col}-1) \end{array} \]

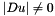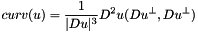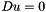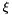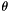All these speculations are based on the hypothesis that $ |Du|\neq 0 $. In fact $ curv(u)=\displaystyle\frac{1}{|Du|^3} D^2u(Du^{\perp}, Du^{\perp})$, which means that, if $ Du = 0$, the Mean Curvature Motion is undefined and has no sense talking about $ \xi $ or $ \theta $. Numerically, even if the gradient is 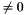$\neq 0 $, but small in modulus, its direction becomes substantially random, because it will be driven by rounding and approximation errors.

These considerations bring us to replace 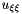$u_{\xi\xi} $ by half the laplacian, if 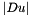$ |Du| $ is below a given threshold (experimentally set to $ 4 $).

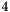Parameters:
[out] ptr_out pointer to the output array
[in] ptr_in pointer to the input array
[in] n_row number of rows
[in] n_col number of columns
[in] dt time step
[in] t_g threshold for the gradient

Definition at line 281 of file FDS_MCM.c.

Here is the call graph for this function:

Here is the caller graph for this function:

Generated on Thu Sep 1 15:24:06 2011 for fds_mcm by  doxygen 1.6.3