• article
• demo
• archive

@article{ipol.2011.llmps-scb,
    title   = {{Simplest Color Balance}},
    author  = {Limare, Nicolas and Lisani, Jose-Luis and Morel, Jean-Michel and Petro, Ana Belén and Sbert, Catalina},
    journal = {{Image Processing On Line}},
    volume  = {1},
    year    = {2011},
    doi     = {10.5201/ipol.2011.llmps-scb},
}
% if your bibliography style doesn't support doi fields:
    note    = {\url{http://dx.doi.org/10.5201/ipol.2011.llmps-scb}}

Communicated by Yann Gousseau
Demo edited by Jose-Luis Lisani

• Nicolas Limare nicolas.limare@cmla.ens-cachan.fr, CMLA, ENS Cachan
• Jose-Luis Lisani joseluis.lisani@uib.es, TAMI, Universitat de les Illes Balears
• Jean-Michel Morel morel@cmla.ens-cachan.fr, CMLA, ENS Cachan
• Ana Belén Petro anabelen.petro@uib.es, TAMI, Universitat de les Illes Balears
• Catalina Sbert catalina.sbert@uib.es, TAMI, Universitat de les Illes Balears

Overview

Color balance algorithms attempt to correct underexposed images, or images taken in artificial lights or special natural lights, such as sunset.

There are many sophisticated algorithms in the literature performing color balance or other color contrast adjustments. The performance of these many color correction algorithms can be evaluated by comparing their result to the simplest possible color balance algorithm proposed here. The assumption underlying this algorithm is that the highest values of R, G, B observed in the image must correspond to white, and the lowest values to obscurity. If the photograph is taken in darkness, the highest values can be significantly smaller than 255. By stretching the color scales, the image becomes brighter. If there was a colored ambient light, for example electric light where R and G dominate, the color balance will enhance the B channel. Thus the ambient light will lose its yellowish hue. Although it does not necessarily improve the image, the simplest color balance always increases its readability.

The algorithm simply stretches, as much as it can, the values of the three channels Red, Green, Blue (R, G, B), so that they occupy the maximal possible range [0, 255]. The simplest way to do so is to apply an affine transform ax+b to each channel, computing a and b so that the maximal value in the channel becomes 255 and the minimal value 0.

However, many images contain a few aberrant pixels that already occupy the 0 and 255 values. Thus, an often spectacular image color improvement is obtained by "clipping" a small percentage of the pixels with the highest values to 255 and a small percentage of the pixels with the lowest values to 0, before applying the affine transform. Notice that this saturation can create flat white regions or flat black regions that may look unnatural. Thus, the percentage of saturated pixels must be as small as possible.

The proposed algorithm therefore provides both a white balance and a contrast enhancement. However, note that this algorithm is not a real physical white balance: It won't correct the color distortions of the capture device or restore the colors or the real-world scene captured as a photography. Such corrections would require a captured sample of known real-world colors or a model of the lighting conditions.

References

1. Wikipedia contributors, "Color balance", Wikipedia, The Free Encyclopedia (accessed January 14, 2010).
2. Marc Ebner, "Color Constancy", John Wiley & Sons, 2007, p. 104.

Algorithm

The naive color balance is a simple pixel-wise affine transform mapping the input minimum and maximum measured pixel values to the output space extrema. As we explained before, a potential problem with this approach is that two aberrant pixel colors reaching the color interval extrema are enough to inhibit any image transform by this naive color balance.

A more robust approach consists in mapping two values V_min and V_max to the output space extrema, V_min and V_max being defined so that a small user-defined proportion of the pixels get values out of the [V_min, V_max] interval.

Implementation

Our input image is an array of N numeric values in the [min, max] interval. The output is a corrected array of the N updated numeric values. Multiple channel images are processed independently on each channel with the same method.

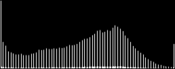
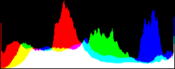
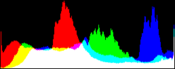
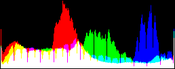
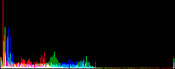
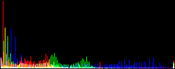
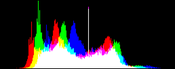
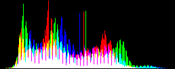
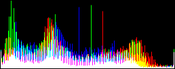
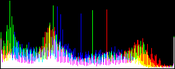
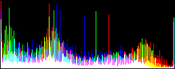
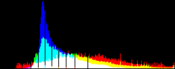
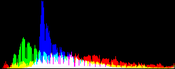
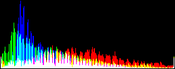
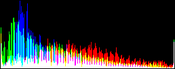
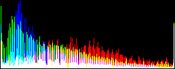
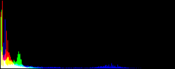
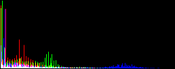
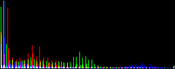
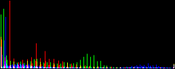
We will perform a color balance on this data where we have saturated a percentage s1% of the pixels on the left side of the histogram, and a percentage s2% of pixels on the right side; for example, s1=0 and s2=3 means that this balance will saturate no pixels at the beginning and will saturate at most N×3/100 at the end of the histogram. We can't ensure that exactly N×(s1+s2)/100 pixels are saturated because the pixel value distribution is discrete.

Sorting Method

V_min and V_max, the saturation extrema, can be seen as quantiles of the pixel values distribution, e.g. first and 99th centiles for a 2% saturation.

Thus, an easy way to compute V_min and V_max is to sort the pixel values, and pick the quantiles from the sorted array. This algorithm would be described as follow:

1. sort the pixel values The original values must be kept for further transformation by the bounded affine function, so the N pixels must first be copied before sorting.
2. pick the quantiles from the sorted pixels With a saturation level s=s1+s2 in [0, 100[, we want to saturate N × s/100 pixels, so V_min and V_max are taken from the sorted array at positions N x s1 / 100 and N x ( 1 - s2 / 100) - 1.
3. saturate the pixels According to the previous definitions of V_min and V_max, the number of pixels with values lower than V_min or higher than V_max is at most N × s/100. The pixels (in the original unsorted array) are updated to V_min (resp. V_max) if their value is lower than V_min (resp. higher than V_max).
4. affine transform The image is scaled to [min, max] with a transformation of the pixel values by the function f such that f(x) = (x - V_min) × (max - min) / (V_max - V_min) + min.

Histogram Method

Sorting the N pixel values requires O(N log(N)) operations and a temporary copy of these N pixels. A more efficient implementation is achieved by an histogram-based variant, faster (O(N) complexity) and requiring less memory (O(max - min) vs. O(N)).

1. build a cumulative histogram of the pixel values The cumulative histogram bucket labeled i contains the number of pixels with value lower or equal to i.
2. pick the quantiles from the histogram V_min is the lowest histogram label with a value higher than N × s1 / 100, and the number of pixels with values lower than V_min is at most N × s1 / 100. If s1 = 0 then V_min is the lowest histogram label, i.e. the minimum pixel value of the input image. V_max is the label immediately following the highest histogram label with a value lower than or equal to N × ( 1 - s2 / 100), and the number of pixels with values higher than V_max is at most N × s2 / 100. If s2 = 0 then V_max is the highest histogram label, i.e. the maximum pixel value of the input image.
3. saturate the pixels
4. affine transform Same as for the sorting method.

Pseudo-code

The following steps presented for images with pixel values in the 8 bit integer space (min = 0, max = 255) with one color channel only. See the following remarks for higher-precision image. Hereafter is the basic implementation, refinements are available in the proposed source code.

image[i] are the pixel values, N is the number of pixels, histo is an array of 256 unsigned integers, with a data type large enough to store N, initially filled with zeros. The arrays indexes start at 0.

// build the cumulative histogram
for i from 0 to N-1
    histo[image[i]] := histo[image[i]] + 1
for i from 1 to 255
    histo[i] := histo[i] + histo[i - 1]
// search vmin and vmax
vmin := 0
while histo[vmin + 1] <= N * s1 / 100
    vmin := vmin + 1
vmax := 255 - 1
while histo[vmax - 1] > N * (1 - s2 / 100)
    vmax := vmax - 1
if vmax < 255 - 1
    vmax := vmax + 1
// saturate the pixels
for i from 0 to N - 1
    if image[i] < vmin
        image[i] := vmin
    if image[i] > vmax
        image[i] := vmax
// rescale the pixels
for i from 0 to N-1
    image[i] := (image[i] - vmin) * 255 / (vmax - vmin)

Higher Precision

For 16 bit integer pixel values, the histogram array method can be used, and needs 65.536 buckets (256 Kb on a 32 bit system, 512 Kb on a 64 bit system, to be compared with the 128 Kb used for a 256×256 image). But the determination of vmin and vmax would benefit of a faster search method, like bisection.

For 32 bit integer pixel values, the histogram size (4.294.967.296 buckets) becomes a problem and can't be properly handled in memory. We can switch to a multi-step process:

• build an histogram with buckets containing more than one single pixel value, such that the histogram size is limited (256 buckets for example, each for a pixel value interval);
• search for the buckets containing vmin and vmax;
• restart the histogram construction and search on a subdivision of these buckets.

If an exact precision isn't required, the latest refinements can be skipped.

For floating-point data, the pixel value can no more be used as an array index, and we must use either a sorting method, or a multi-step method with an histogram containing intervals (not values), then a sorting method on the buckets containing vmin and vmax.

Note that the proposed pseudo-code can also be used for images with integer pixel values (as produced by common image capture devices and found in common image formats) stored as floating-point data (often desired for image processing), by converting the pixel value image[i] to its integer equivalent while filling the histogram.

Special Cases

If the image is constant (all pixels have the same value v), then, according to the described implementation and pseudo-code, the histogram values are 0 for labels lower than v, and N for labels higher or equal to v, and then for any value of s1 and s2 , V_min = v, V_max = v.

This (V_min = V_max) can also happen for non-constant image, the general case being images with less than N × s1 / 100 pixels with values below or with more than N × s2 / 100 above a median value v. This case can be handled by setting all the pixels to the value v.

Color images

RGB Color Balance

For RGB color images we can apply the algorithm independently on each channel. We call this algorithm RGB color balance. The color of the pixels is modified in the process because each RGB channel is transformed by an affine function with different parameters and the saturation does not occur on the three RGB channels together. This can be desirable do correct the color of a light source or filter, but in some applications we may want to maintain the colors of the input image.

In that case, many solutions are possible, depending on how we define the "color" to be maintained (hue, chroma, R/G/B ratio) and what we want to correct with this algorithm (lightness, brightness, intensity, luma, ...). A discussion about these color correction variants will be published in a later article, and we present hereafter the simplest version.

IRGB Intensity Balance

The goal of IRGB intensity balance is to correct the intensity of a color image without modifying the R/G/B ratio of the pixels. We first compute the gray level intensity (I = (R+G+B)/3), then this intensity is balanced and transformed into I' by the affine transformation with saturation. Finally, for each pixel, the three color channels are multiplied by I'/I.

But the RGB color cube is not stable by this transformation. Multiplied by I'/I, some RGB components will be larger than the maximum value. This is corrected in a post-processing step by a projection on the RGB cube while maintaining the R/G/B ratio, ie replacing pixels out of the RGB cube by the intersection of the RGB cube surface and the segment connecting the (0,0,0) point and the pixels to be corrected. This projection has three consequences :

• commutativity : computing the intensity I of an image after correction by this algorithm doesn't give the same result as computing the intensity of an image and correcting this intensity by the affine balance algorithm with saturation described at the beginning of this article;
• monotonicity : some pixels with intensities I₁ < I₂ can be be transformed into pixels with intensities I'₁ > I'₂ if the second pixels has to be corrected by projection;
• precision : because the projection step is darkening the projected pixels, less than s2% of the pixels will have their final intensity saturated to the maximum value.

Moreover, adjusting the saturation on the average I of the three RGB channels means that, unless the three channels are equal (gray image), before the projection less than s2% of the pixels are saturated to the maximum value on the three RGB channels while more than s2% of the pixels are saturated to the maximum value on at least one of the RGB channels.

Better solutions to achieve a balance of a color image without these problems require the use of other color spaces and are beyond the scope of this article.

Online Demo

With the online demonstration, you can try this algorithm on your own images and set the desired percentage of saturated pixels. This demo presents the algorithm applied independently to the R, G and B channels (RGB color balance), and to the intensity channel while maintaining the R/G/B ratio (IRGB intensity balance).

For gray-scale images, these two versions are identical to applying the simple algorithm to the gray level.

Source Code

An ANSI C implementation is provided and distributed under the GPL license: source code, documentation (online)

Basic compilation and usage instructions are included in the README.txt file. This code requires the libpng library.

• Linux. You can install libpng with your package manager.
• Mac OSX. You can get libpng from the Fink project.
• Windows. Precompiled DLLs are available online for libpng.

This source code includes two implementations of the color balance: a 8bit integer implementation based on the histogram algorithm with O(N) complexity and a lookup table for fast affine transform is used for the RGB color balance, and a generic floating-point implementation based on qsort(), with O(N log(N)) algorithmic complexity is used for the IRGB intensity balance.

The histogram code is used for the online demo. The source code history and future releases are available on an external page

Examples

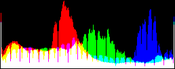
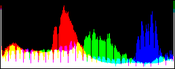
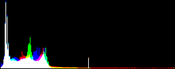
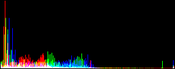
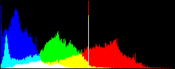
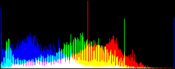
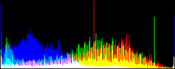
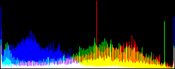
We show from left to right the original image, and its result by RGB color balance with 0%, 1%, 2% and 3% of the pixels saturated, half at the beginning of the histogram and half at the end of the histogram. In this example, the algorithm has been applied independently on each color channel. It is quite apparent that some saturation is almost always necessary, but that the needed percentage is variable.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

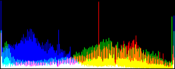Here, the 0% saturation already gives a result, and 1% is optimal. Notice how the orange ambient light has been corrected to more daylight image.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

histograms

In fact, a white thin rim surrounds this image! This rim occupies more than 2% of the image. Hence, the 3% threshold is the right one.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

histograms

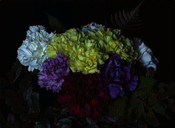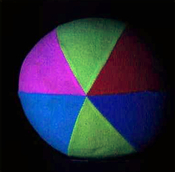
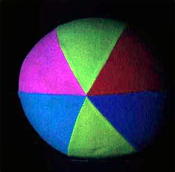
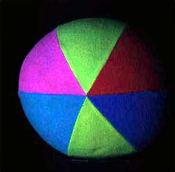
Like the preceding ones, this image in completely unnatural blue light is often used to illustrate color balance, or color contrast adjustment algorithms. A trivial affine transform corrects it adequately by removing the bluish effect. A still more contrasted result is obtained by saturating only 1%.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

histograms

The same remarks as for the preceding one apply to this image.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

histograms

Even a good quality image can benefit from a moderate 1% color balance. A contrast improvement is noticeable when switching between the 0% and 1% versions.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

histograms

There is no real good solution for this sunset image. The colors are strongly blue/orange and will stay so. By pushing too far the saturation (3%), the orange pixels diminish and a completely unnatural blue color is created.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

histograms

This image and the following two have been used in recent papers on color perception theory (Retinex).

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

histograms

Examples on Gray-scale Images

We present two examples on grayscale images. The algorithm is the same, since the three channels are equal. In the first image we observe a small improvement of the image. In the second, the improvement is more significant, but we lose the little details in the image.

original image	balanced 3%

original image	balanced 1%	balanced 3%

Examples with Little or no Improvement

Here, it is probably best not to apply any color balance: the colors become quickly unearthly.

original image	balanced 0%	balanced 1%	balanced 2%	balanced 3%

The following image with back-lighting has no simple solution.

original image	balanced 3%

original image	balanced 3%

image credits